Skip to main content

Polyominoes, Polygons, and Polyhedra: Discovering Geometry through Exploration

Teresa D. Magnus

Section 3.3 Prisms and Cylinders

Subsection 3.3.1 Definitions

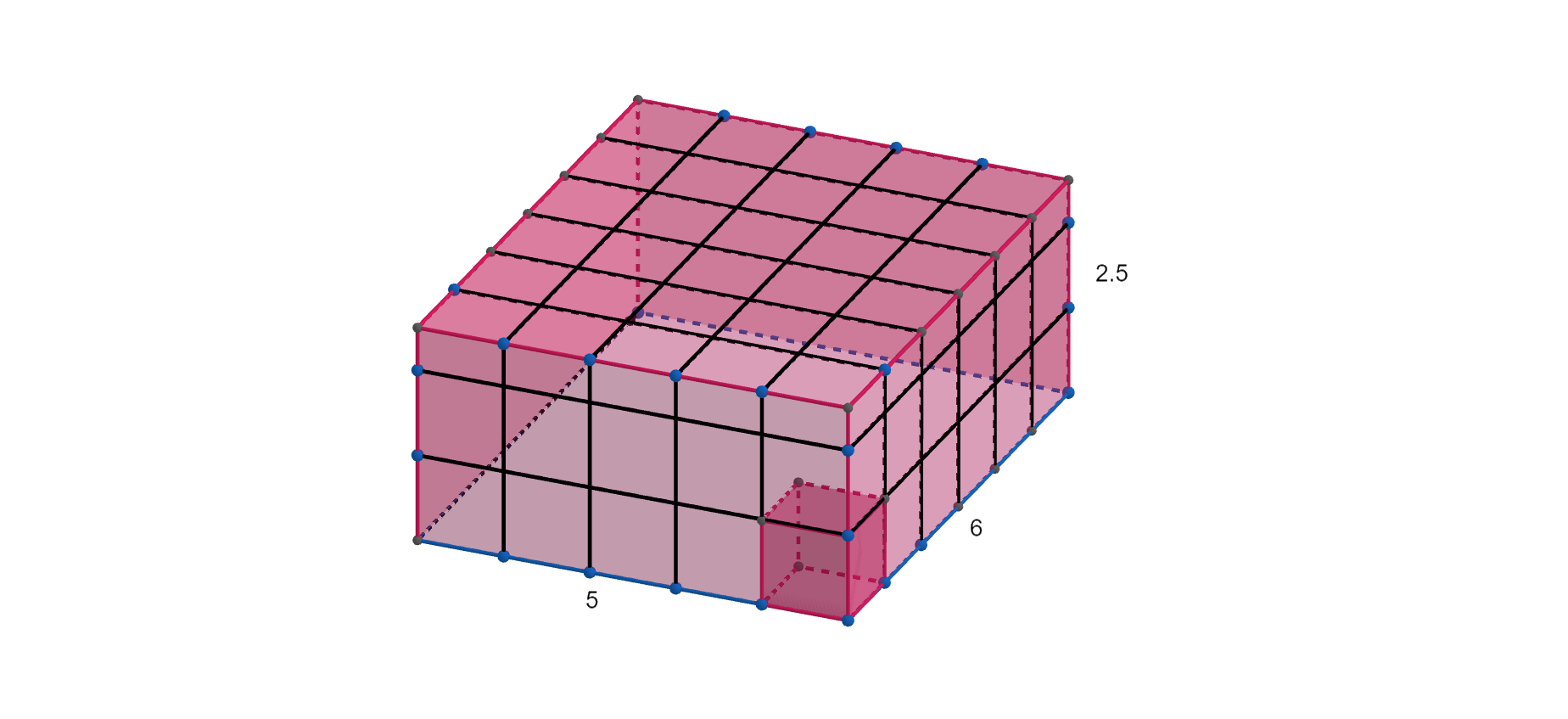
We now explore the geometric solid known as a prism in greater detail. As noted in Definition 3.2.7, a prism is a box-like geometric solid with a pair of congruent and parallel polygonal faces, called the base and the summit, joined by a band of parallelograms. The number of parallelograms connecting the bases will always equal the number of sides of each base.
We are most familiar with right prisms, namely prisms where the bases meet all the side faces at right angles; the side faces of a right prism are rectangles. An oblique prism, on the other hand, will have parallelograms rather than rectangles as its side faces.
A rectangular box.
(a) Right Prism
(b) Oblique Prism
Figure 3.3.1. Right and Oblique Prisms
A cylinder is not a polyhedron since it has circular bases; however, there are some important similarities between prisms and cylinders. Both have parallel, congruent bases.
A cylinder or can.
(a) Right Cylinder
A can that is oblique.
(b) Oblique Cylinder
Figure 3.3.2. Right and Oblique Cylinders

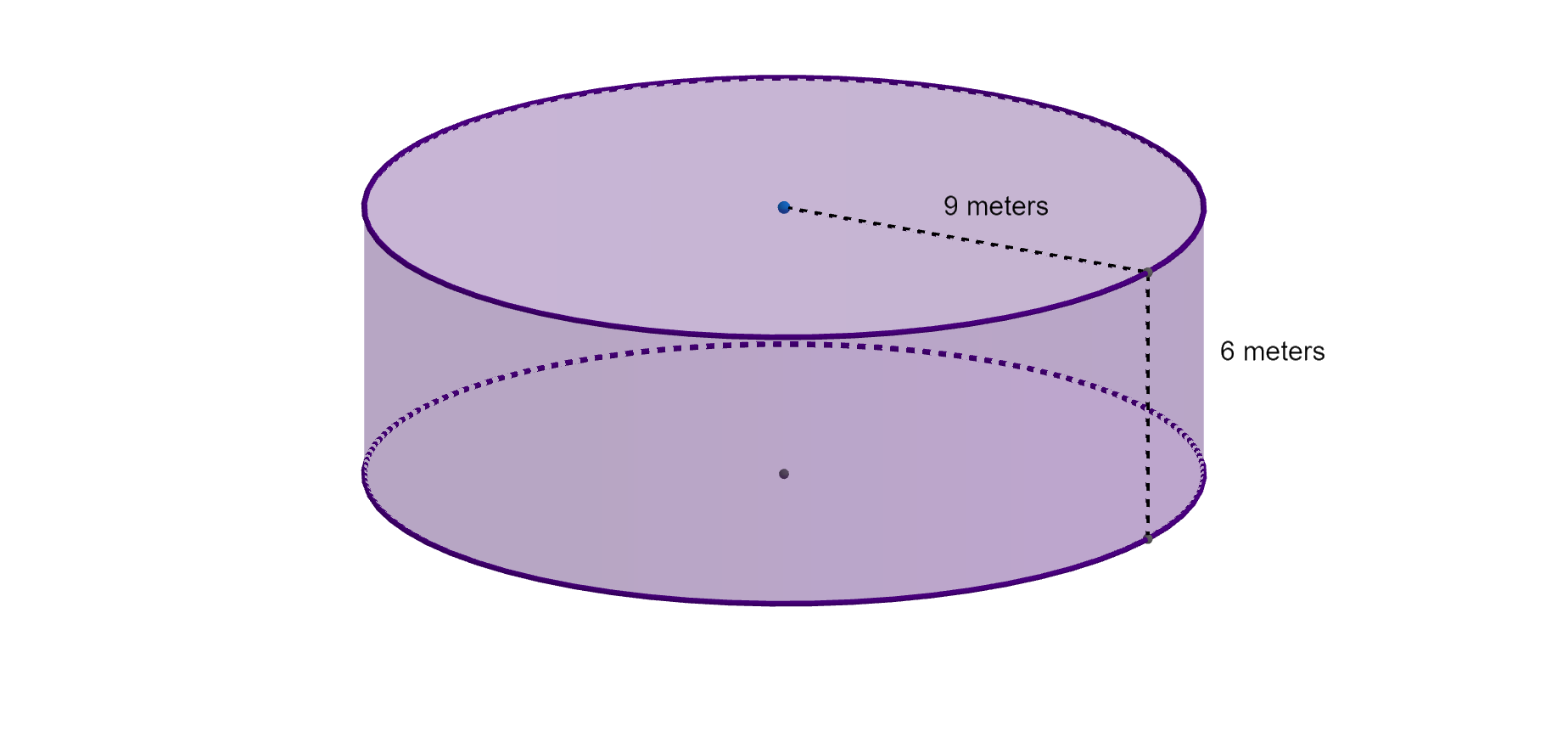
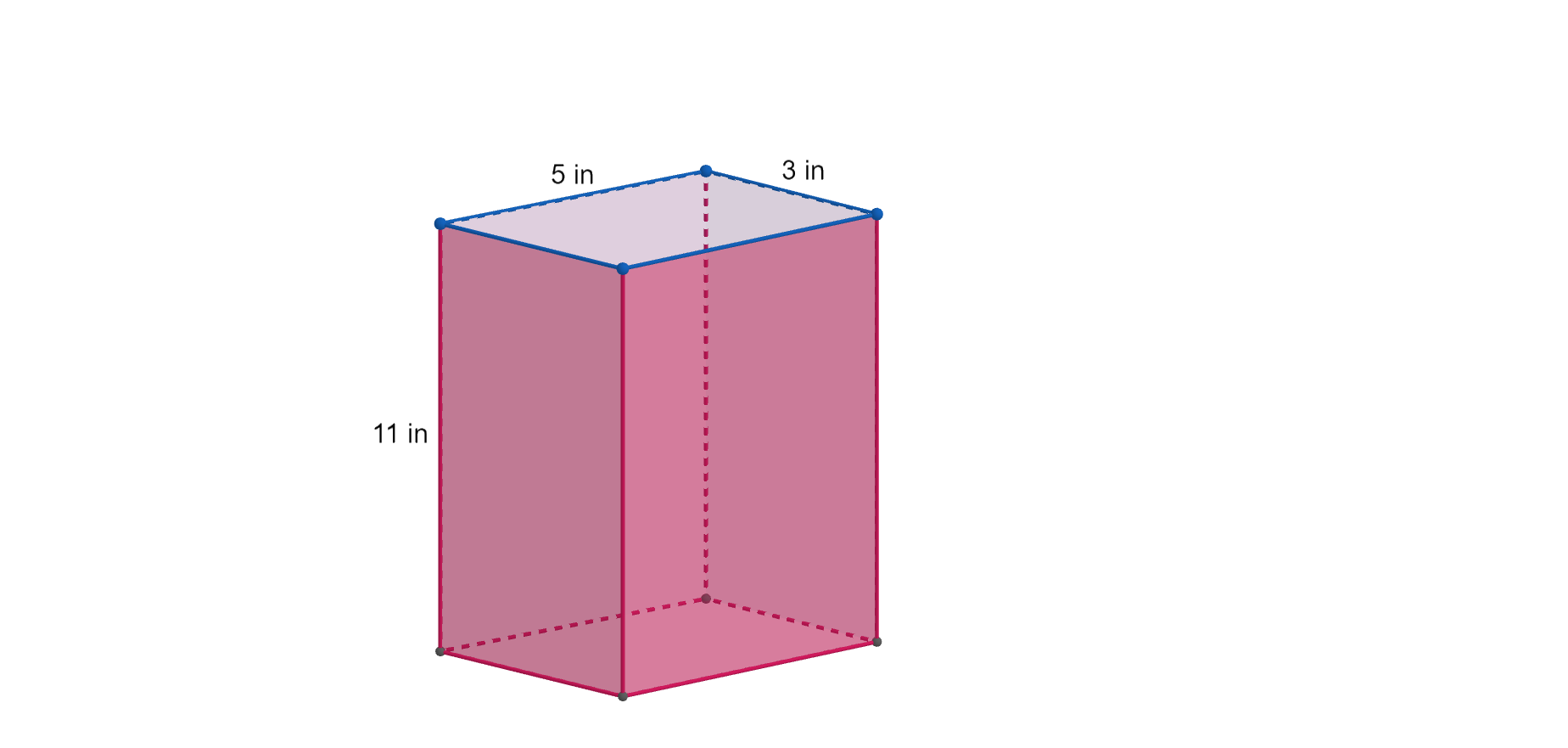
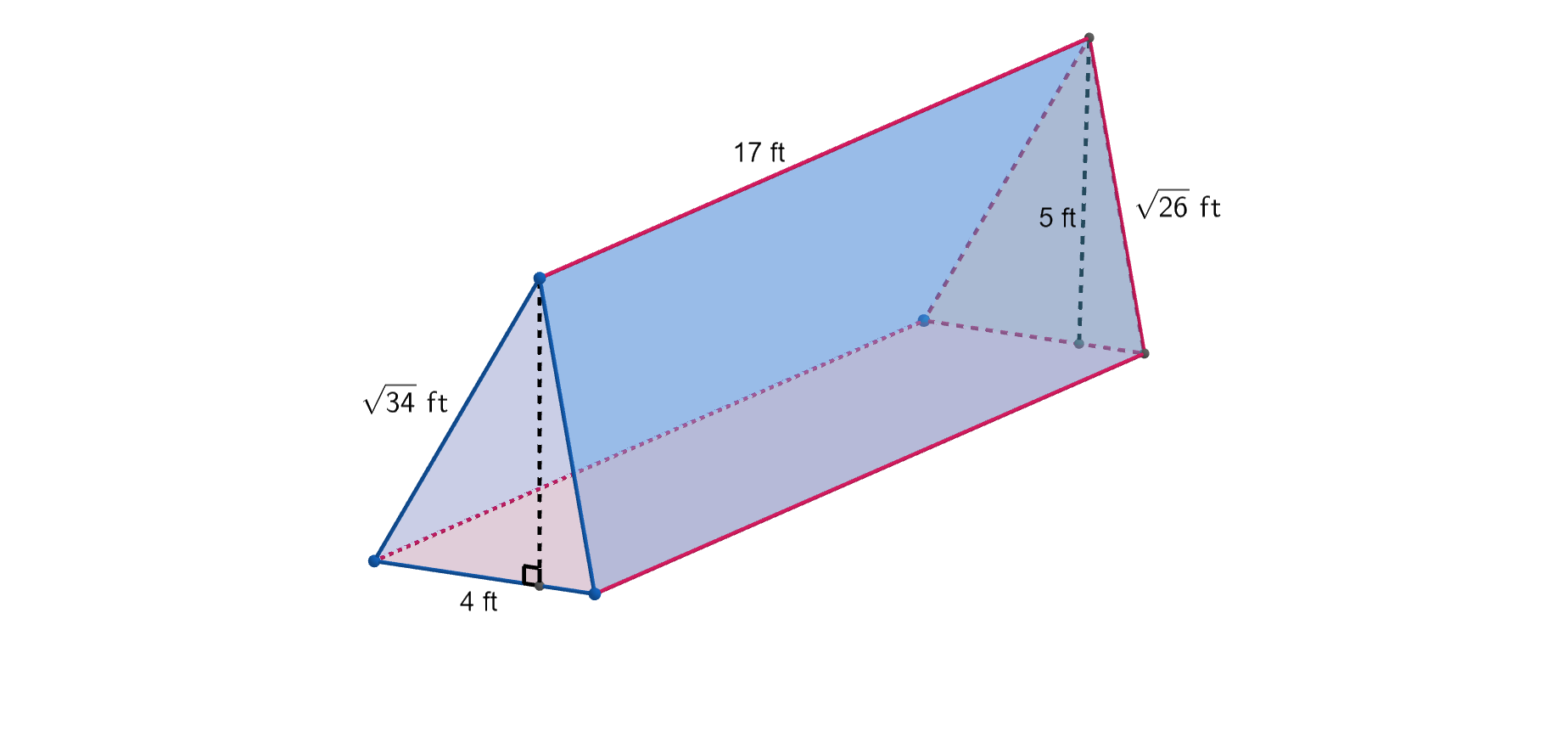
Checkpoint 3.3.3. Check your understanding.

Besides the parallel circles, what other shape(s) is needed to form the surface of a right cylinder? How many of these shapes are there?
Hint.
Cut two circles out of paper to cover a cylindrical can. What else do you need to cover the exposed surface?
Answer.
The two circles are joined by a single rectangle. The width of this rectangle equals the circumference of a circular end.
An important measurement for prisms and cylinders is the distance between the bases. Many geometry textbooks use the term height to describe this distance.

Definition 3.3.4.

The height of a prism or cylinder is the distance between the parallel congruent bases and is measured along a line perpendicular to the bases. When a prism or cylinder is sitting on a side other than a base, the height will be measured laterally instead of vertically. In this text, the word stretch will be used in lieu of ‘height’ to clarify which dimension is being discussed.
The stretch (or height) of a right prism is usually measured along an edge of one of the rectangular sides, like \(d\) in Figure 3.3.1.(a). On the other hand, the stretch of a skew prism, such as the one illustrated in Figure 3.3.1.(b), will be less than the height of a side face. Similarly, the stretch of a cylinder is also measured at a right angle to the base as indicated by \(d\) in Figure 3.3.2.

Subsection 3.3.2 Volumes of Prisms and Cylinders

In this exploration, we learn how to measure the space inside of a prism or pyramid. Hopefully, exploring the meaning of volume will help you appreciate and remember how to find volume.

Exploration 3.3.1. Understanding Volume.

(a)
Suppose you have a box (right rectangular prism) that has a height (or stretch) of 6 inches, a length of 5 inches, and a width of 7 inches and you have a large supply of \(1''\times 1''\times 1''\)-cubes.
  1. If you cover the bottom of the inside of the box with a single layer of \(1''\times 1''\times 1''\)-cubes, how many cubes will fit in this first layer?
  2. How many horizontal layers of \(1''\times 1''\times 1''\)-cubes could you fit in the box? Would each of these layers contain the same number of cubes as the first layer?
  3. What is the total number of 1”x1”x1”-cubes that could fit in the box?
(b)
Explain why the formula for the volume of a rectangular box is \(V=\ell wh\) where \(\ell\) is the length, \(w\) is the width, and \(h\) is the height of the box.
(c)
When \(h\) is a whole number, it makes sense to think about the height as the number of layers. Not all measurements are whole numbers though. Instead we can think of \(h\) as the amount that we need to stretch that first layer to reach the summit of the prism. Consider the rectangular prism in Figure 3.3.5 with base dimensions, \(\ell=5\) inches and \(w=6\) inches, and a stretch of \(d=2.5\) inches. Find the volume of the prism.
A prism.
Figure 3.3.5. A prism with dimensions 5x6x2.5.
(d)
This notion of stretching the bottom layer holds for all prisms and cylinders, not just rectangular ones. Suppose a cylinder has a circular base with area 9.4 square centimeters. If the cylinder is one centimeter tall, we will say that the volume is \(9.4\times 1=9.4\) cubic centimeters.
  1. If the cylinder is two centimeters tall, how should the volume compare to that of the one-centimeter-tall cylinder with the same base? What is the volume?
  2. If the cylinder is three centimeters tall, what is the volume?
  3. If the cylinder is five centimeters tall, what is the volume?
  4. If the cylinder is 7.5 centimeters tall, what is the volume?
  5. If the cylinder is \(d\) centimeters tall, what is volume?
Exploration Understanding Volume showed that the volume of a prism or cylinder was equal to the area of the base times the number of horizontal layers. Although you may be familiar with the formula \(V=\ell wh\text{,}\) it is preferable to have a single formula that allows us to compute the volume of all prisms, not just rectangular prisms. Note that the formula \(V=(\ell w)d\) is equivalent to the formula \(V=Ad\) where \(A=\ell w\) is the area of one base of a rectangular prism and \(d\) is the distance (or stretch) between the bases, measured perpendicular to the bases. This volume formula \(V=Ad\) will extend to all prisms and even cylinders! Much less to memorize! To find the volume of any prism or cylinder, whether right or oblique, we need only compute the area of the base and then multiply this area by the stretch between the bases.

Exploration 3.3.2. Finding the Volume of Prisms and Cylinders.

(a)
Use the formula \(V=Ad\) to determine the volume of the right prism Figure 3.3.6 with an isosceles triangle base.
Prism with isosceles triangle bases. Triangles have base 12 feet and height 14 feet. Distance between the bases is 18 feet.
Figure 3.3.6. Isosceles triangle right prism
(b)
Show all work as you compute the following measurements for the oblique cylinder in Figure 3.3.7. Formulas for the area and circumference of a circle are given in Definition 2.1.8.
(i)
The stretch \(d\text{.}\)
(ii)
The area of a circular base.
Hint.
The answers involve irrational numbers, namely a square root and \(\pi\text{.}\)
(iii)
The volume of the cylinder.
Hint.
Your answer to will be more accurate if you use the actual square root and \(\pi\text{,}\) not their estimates, in your calculation of volume. If you do use estimates, include at least four digits after the decimal point when inputting the values.
(c)
Create a formula for the volume of a cylinder with height \(h\) where the radius of each circular base is \(r\text{.}\) Your formula should contain the variables \(h\) and \(r\text{.}\) Then check that your formula gives the same result as you found in Task 3.3.2.b.

Subsection 3.3.3 The Surface Area of Prisms and Cylinders

While the volume measures the amount of interior space of a 3-dimensional solid, the surface area measures the amount of material needed to create the shell or surface of the solid. To compute surface area, we simply compute the area of each face and add the areas together.

Definition 3.3.8.

The surface area of a geometrical solid is the sum of the areas of the surfaces that bound the solid.

Exploration 3.3.3. Finding the Surface Area of Prisms and Cylinders.

(a)
The triangular prism in Figure 3.3.6 has five faces. Determine the area of each face and then compute the surface area.
(b)
The right cylinder in Figure 3.3.9 has a height of 20 ft. and a diameter of 10 ft.
  1. Determine the area of each circular base.
  2. With the circular ends removed, the cylinder looks like a tube, perhaps the cardboard center of a paper towel or toilet paper roll. If we cut this tube lengthwise
     1 
    Here, lengthwise means a long a line perpendicular to an edge.
    and flatten it out, what shape do we get?
  3. To determine the area of this flattened surface, we will need to determine its dimensions. One of these dimensions will be the length of the once-circular edge. What is the other dimension?
  4. To find the length of the once-circular edge, we note that this edge was the circumference of the circular base. Determine this length. Then determine the area of the flattened surface.
  5. Add the areas of the three surfaces of the cylinder, namely the two circular bases and the flattened tube, to compute the surface area of the cylinder.
Right cylinder with height 20 feet and diameter 10 ft.
Figure 3.3.9. A right cylinder
(c)
Create a general formula for a right cylinder with height \(h\) where the radius of each circular base is given by the variable \(r\text{.}\) Your formula should contain the variables \(h\) and \(r\text{.}\) Then check that your formula gives the same result as you found in Task 3.3.3.b for the surface area of the cylinder in Figure 3.3.9.

Exercises 3.3.4 Exercises

Building Our Toolbox

As you add these items to your toolbox, you are encouraged to write them in a form that is clear, thorough, and meaningful to you so that you can refer to them later.
1.
What is a prism? What is a cylinder? How are they similar? How do they differ?
2.
In your own words, describe what volume means. Then explain how you find the volume of prisms and cylinders. You may include formula(s) and example(s). Make sure that your response covers all types of prisms as well as cylinders.
3.
In your own words, describe what surface area means. Then explain how you find the surface area of prisms and cylinders. You may include formula(s) and example(s). Make sure that your response covers all types of prisms as well as cylinders.

Skills and Recall

4.
Determine the volumes of the following prisms and cylinders:
  1. A rectangular box with length 8 cm, width 3 cm, and height 10 cm.
  2. A triangular prism where the stretch is 6 inches and each base is a 3-4-5 (inch) right triangle.
  3. A cylinder with radius 15 inches and height 4 inches.
5.
Determine the volumes of the prisms and cylinders sketched below.
  1. The cylinder in Figure 3.3.10
  2. The rectangular prism in Figure 3.3.11
  3. The triangular prism in Figure 3.3.12
A cylinder with height 6 meters and radius 9 meters.
Figure 3.3.10. Cylinder
A rectangular prism with height 11 inches, width 5 inches, and length 3 inches.
Figure 3.3.11. Rectangular prism
Triangular prism with stretch 17. Triangle has a base length of 4, slant lengths of square root 34 and square root 26, and a height of 5.
Figure 3.3.12. Triangular prism

Extending the Concepts

8. Measuring a Pentagonal Prism.
The face \(ABCDE\) of the right pentagonal prism in Figure 3.3.13 has right angles \(\angle{EAB}\) and \(\angle{ABC}\text{.}\) Segment \(\overline{DF}\) is an altitude for the pentagon meeting \(\overline{AB}\) at point \(F\text{.}\) The lengths of the sides of \(ABCDE\) are the same as those shown for the summit \(KLMNO\text{,}\) namely
  • \(\displaystyle AB=10\)
  • \(\displaystyle BC=AE=4\)
  • \(\displaystyle CD=DE=\sqrt{41}\approx 6.4\)
In addition, but not shown, \(\overline{EC}\) is a perpendicular bisector of \(\overline{FD}\text{.}\) The distance between the base and summit pentagon is \(LB=10\text{.}\)
  1. Determine the volume of this pentagonal prism. Include your work and reasoning.
  2. On graph paper, sketch a net for this pentagonal prism.
  3. Determine the surface area of the pentagonal prism.
Hint.
There will be a slight variation in answers depending on whether you use \(\sqrt{41}\) or 6.4 in your work.
9.
In Figure 3.3.14, a cylinder can be formed by joining the edges \(\overline{CG}\) and \(\overline{DF}\) and then folding in the two circles. The side \(\overline{GF}\) has length \(3.6\pi\approx 11.3\) and side \(\overline{DF}\) has length 6.
(a)
How is the length of segment \(\overline{GF}\) related to the circle with center \(J\text{?}\)
Hint.
Segment \(\overline{GF}\) should wrap around the circle. To what measurement of a circle does this correspond?
(b)
Determine the area of the circle with center \(J\text{.}\)
(c)
Determine the surface area of the cylinder.
(d)
Determine the volume of the cylinder.
PrevTopNext